সরলরেখায় গতি:
২.১ ভূমিকা
বস্তুবিজ্ঞানে গতি একটি সাধারণ বিষয়। আমরা হাঁটি, দৌড়াই এবং সাইকেল চালাই। এমনকি ঘুমানোর সময়েও, বাতাস আমাদের ফুসফুসে প্রবেশ করে এবং বেরিয়ে আসে, এবং রক্ত ধমনী ও শিরার মাধ্যমে প্রবাহিত হয়। আমরা গাছ থেকে পাতা পড়তে এবং বাঁধ থেকে জল প্রবাহিত হতে দেখি। যানবাহন এবং উড়োজাহাজ মানুষকে এক স্থান থেকে অন্য স্থানে নিয়ে যায়। পৃথিবী প্রতি চব্বিশ ঘণ্টায় একবার নিজ অক্ষে ঘুরে এবং প্রতি বছরে সূর্যের চারপাশে পরিভ্রমণ করে। সূর্য নিজেই মিল্কিওয়ে গ্যালাক্সিতে গতি করছে, যা আবার স্থানীয় গ্যালাক্সি গ্রুপের মধ্যে চলছে।
গতি হল সময়ের সাথে সাথে কোনো বস্তুর অবস্থানের পরিবর্তন। কীভাবে অবস্থান সময়ের সাথে পরিবর্তিত হয়? এই অধ্যায়ে আমরা গতি বর্ণনা করতে শিখব। এর জন্য আমরা বেগ এবং ত্বরণের ধারণা গড়ে তুলব। আমরা সরল রেখার সাথে সম্পর্কিত বস্তুর গতির অধ্যয়নেই সীমাবদ্ধ থাকব, যা রৈখিক গতি (rectilinear motion) নামে পরিচিত। অভিন্ন ত্বরণের ক্ষেত্রে রৈখিক গতির জন্য একটি সহজ সমীকরণ সেট করা যায়। অবশেষে, গতির আপেক্ষিক প্রকৃতি বোঝার জন্য আমরা আপেক্ষিক বেগের ধারণা প্রবর্তন করব।
গতি বিশ্বব্রহ্মাণ্ডের প্রতিটি জিনিসের সাধারণ বৈশিষ্ট্য। আমরা হাঁটি, দৌড়াই এবং সাইকেল চালাই। এমনকি ঘুমানোর সময়ও, বাতাস আমাদের ফুসফুসে প্রবেশ করে এবং বেরিয়ে আসে, এবং রক্ত ধমনী ও শিরার মাধ্যমে প্রবাহিত হয়। আমরা গাছ থেকে পাতা পড়তে এবং বাঁধ থেকে জল প্রবাহিত হতে দেখি। যানবাহন এবং উড়োজাহাজ মানুষকে এক স্থান থেকে অন্য স্থানে নিয়ে যায়। পৃথিবী প্রতি চব্বিশ ঘণ্টায় একবার নিজ অক্ষে ঘুরে এবং প্রতি বছরে সূর্যের চারপাশে পরিভ্রমণ করে। সূর্য নিজেই মিল্কিওয়ে গ্যালাক্সিতে গতি করছে, যা আবার স্থানীয় গ্যালাক্সি গ্রুপের মধ্যে চলছে।
গতি হল সময়ের সাথে সাথে কোনো বস্তুর অবস্থানের পরিবর্তন। কীভাবে অবস্থান সময়ের সাথে পরিবর্তিত হয়? এই অধ্যায়ে আমরা গতি বর্ণনা করতে শিখব। এর জন্য আমরা বেগ এবং ত্বরণের ধারণা গড়ে তুলব। আমরা সরল রেখার সাথে সম্পর্কিত বস্তুর গতির অধ্যয়নেই সীমাবদ্ধ থাকব, যা রৈখিক গতি (rectilinear motion) নামে পরিচিত। অভিন্ন ত্বরণের ক্ষেত্রে রৈখিক গতির জন্য একটি সহজ সমীকরণ সেট করা যায়। অবশেষে, গতির আপেক্ষিক প্রকৃতি বোঝার জন্য আমরা আপেক্ষিক বেগের ধারণা প্রবর্তন করব।
আমাদের আলোচনায়, চলমান বস্তুগুলোকে বিন্দু বস্তু হিসেবে বিবেচনা করা হবে। এই ধারণা তখনই সঠিক থাকে, যখন বস্তুর আকার তার গতিশীল সময়ে অতিক্রান্ত দূরত্বের তুলনায় অনেক ছোট হয়। বাস্তব জীবনের অনেক ক্ষেত্রে, বস্তুর আকার উপেক্ষা করা যায় এবং এগুলোকে বিন্দু সদৃশ বস্তু হিসেবে বিবেচনা করা যেতে পারে, যেখানে ত্রুটি কম হয়।
কাইনেম্যাটিকস-এ আমরা গতির কারণের গভীরে না গিয়ে কেবল গতি বর্ণনার উপায়গুলি অধ্যয়ন করি। গতির কারণ অধ্যয়ন পরবর্তী অধ্যায় (অধ্যায় ৪)-এ অন্তর্ভুক্ত করা হয়েছে।
2.2 তাৎক্ষণিক বেগ এবং গতি
গড় বেগ আমাদের জানায় একটি বস্তু একটি নির্দিষ্ট সময় অন্তরালে কত দ্রুত গতিতে চলেছে, কিন্তু এটি আমাদের জানায় না যে সেই সময়ের অন্তরালে বিভিন্ন মুহূর্তে বস্তুটি কত দ্রুত চলেছে। এর জন্য, আমরা তাৎক্ষণিক বেগ বা সহজভাবে বললে, একটি নির্দিষ্ট মুহূর্ত t-এ বেগ সংজ্ঞায়িত করি।
কোনো নির্দিষ্ট মুহূর্তের বেগ সংজ্ঞায়িত হয় গড় বেগের সীমা হিসেবে, যখন সময় অন্তরাল অসীম ক্ষুদ্র হয়ে যায়। অর্থাৎ,
(2.1a)
(2.1b)
এখানে, চিহ্নটি নির্দেশ করে যে ডানপাশে থাকা পরিমাণটির জন্য শূন্যে গিয়ে সীমা নেওয়ার কাজ। ক্যালকুলাসের ভাষায়, সমীকরণ (2.1a)-এর ডানপাশে থাকা পরিমাণটি -এর তুলনায় -এর অন্তরকলকের (differential coefficient) প্রতিনিধিত্ব করে এবং এটি দ্বারা চিহ্নিত হয় (অধ্যায় ২.১ দেখুন)। এটি একটি নির্দিষ্ট মুহূর্তে সময়ের তুলনায় অবস্থানের পরিবর্তনের হার।
আমরা সমীকরণ (2.1a) ব্যবহার করে তাৎক্ষণিক বেগের মান গ্রাফিক্যালি বা গাণিতিকভাবে বের করতে পারি। ধরা যাক, আমরা গাড়ির গতির জন্য Fig. 2.1-এ প্রদর্শিত গতির রেখার উপর সময় সেকেন্ডে (বিন্দু P) বেগের মান বের করতে চাই।
আমরা সেকেন্ড ধরে নিই, যা সেকেন্ডে কেন্দ্রীভূত। এরপর, গড় বেগের সংজ্ঞা অনুযায়ী, রেখা -এর ঢাল (Fig. 2.1) ৩ সেকেন্ড থেকে ৫ সেকেন্ড পর্যন্ত সময় অন্তরালের গড় বেগের মান দেয়।
চিত্র 2.1: অবস্থান-সময় গ্রাফ থেকে বেগ নির্ধারণ। -এ বেগ হল ঐ মুহূর্তে গ্রাফের স্পর্শকের ঢাল।
এখন, আমরা -এর মান ২ সেকেন্ড থেকে ১ সেকেন্ডে কমাই। তখন রেখা -তে পরিণত হয় এবং এর ঢাল ৩.৫ সেকেন্ড থেকে ৪.৫ সেকেন্ড পর্যন্ত সময়ের মধ্যে গড় বেগের মান দেয়। সীমা -এ, রেখা অবস্থান-সময় বক্ররেখায় বিন্দু -তে স্পর্শকে পরিণত হয় এবং -এ বেগ হল ঐ বিন্দুতে স্পর্শকের ঢাল।
এই প্রক্রিয়াটি গ্রাফিকভাবে দেখানো কঠিন। তবে, যদি আমরা গাণিতিক পদ্ধতি ব্যবহার করে বেগের মান বের করি, সীমা প্রক্রিয়ার অর্থ আরও পরিষ্কার হয়। চিত্র 2.1-এ দেখানো গ্রাফের জন্য ।
টেবিল 2.1-এ এর মান ২.০ সেকেন্ড, ১.০ সেকেন্ড, ০.৫ সেকেন্ড, ০.১ সেকেন্ড এবং ০.০১ সেকেন্ড ধরে -এ কেন্দ্র করে -এর মান দেখানো হয়েছে। দ্বিতীয় ও তৃতীয় কলামে এবং -এর মান এবং চতুর্থ ও পঞ্চম কলামে সংশ্লিষ্ট -এর মান, অর্থাৎ এবং দেওয়া হয়েছে। ষষ্ঠ কলামে পার্থক্য এবং শেষ কলামে -এর মান, অর্থাৎ গড় বেগ, -এর মান অনুযায়ী দেখানো হয়েছে।
টেবিল 2.1 থেকে আমরা দেখতে পাই যে, যখন -এর মান ২.০ সেকেন্ড থেকে ০.০১ সেকেন্ডে কমে, গড় বেগের মান সীমা মান -এর দিকে ধাবিত হয়, যা -এ বেগের মান, অর্থাৎ -এর মান। এই পদ্ধতিতে, আমরা গাড়ির গতির জন্য প্রতিটি মুহূর্তে বেগ গণনা করতে পারি।
তাৎক্ষণিক বেগ নির্ধারণের জন্য গ্রাফিক পদ্ধতি সবসময় সুবিধাজনক নয়। এর জন্য, আমাদের অবশ্যই সতর্কতার সাথে অবস্থান-সময় গ্রাফ অঙ্কন করতে হবে এবং -এর মান ছোট থেকে ছোট করার সাথে গড় বেগের মান গণনা করতে হবে।
যদি বিভিন্ন মুহূর্তে অবস্থানের ডেটা থাকে বা অবস্থানের সময়ের উপর নির্ভরশীল সঠিক প্রকাশ থাকে, তাহলে বিভিন্ন মুহূর্তে বেগ গণনা করা সহজ। এরপর আমরা ডেটা থেকে -এর মান গণনা করি, -এর মান ছোট করি এবং টেবিল 2.1-এ যেমন করা হয়েছে, সীমা মান খুঁজে বের করি বা প্রদত্ত প্রকাশের জন্য ডিফারেনশিয়াল ক্যালকুলাস ব্যবহার করি এবং বিভিন্ন মুহূর্তে -এর মান বের করি, যেমন নিম্নলিখিত উদাহরণে দেখানো হয়েছে।
উদাহরণ 2.1
একটি বস্তু x-অক্ষে চলাচল করছে, যার অবস্থান দেওয়া আছে দ্বারা। এখানে , , এবং সেকেন্ডে পরিমাপ করা হয়। এবং -এ এর বেগ কত? এবং -এর মধ্যে গড় বেগ কত?
উত্তর:
ডিফারেনশিয়াল ক্যালকুলাসের চিহ্নন পদ্ধতিতে বেগ হলো:
এখানে ।
তাহলে, ।
-এ, এবং -এ,
এবং -এর মধ্যে গড় বেগ:
এখানে,
তাহলে,
এবং,
তাহলে,
দ্রষ্টব্য:
যদি গতি অভিন্ন হয়, তবে বেগ সব মুহূর্তে গড় বেগের সমান হয়।
তাত্ত্বিক বিশ্লেষণ:
তাৎক্ষণিক গতি বা গতি হলো বেগের মান। উদাহরণস্বরূপ, এবং -এর গতি একই, যা ।
২.৩ ত্বরণ
একটি বস্তুর বেগ, সাধারণভাবে, তার চলাচলের সময় পরিবর্তিত হয়। এই পরিবর্তন কীভাবে বর্ণনা করা হবে? এটি কি বেগের পরিবর্তন হারকে দূরত্বের সাথে না সময়ের সাথে বিবেচনা করা উচিত?
এটি গ্যালিলিওর সময়েও একটি সমস্যা ছিল। প্রথমে মনে করা হয়েছিল যে বেগের পরিবর্তন হারকে দূরত্বের সাথে বর্ণনা করা যেতে পারে। কিন্তু, পতনশীল বস্তু এবং ঢালু সমতলে চলমান বস্তুর গতির উপর গবেষণা করে, গ্যালিলিও সিদ্ধান্তে পৌঁছেছিলেন যে সময়ের সাথে বেগের পরিবর্তন হার সমস্ত পতনশীল বস্তুর জন্য একটি ধ্রুবক।
গড় ত্বরণ
গড় ত্বরণ একটি সময় অন্তরালে বেগের পরিবর্তন হারকে বর্ণনা করে:
এখানে এবং হলো এবং -এ তাৎক্ষণিক বেগ। SI একক হলো ।
তাৎক্ষণিক ত্বরণ
তাৎক্ষণিক ত্বরণ হলো:
ত্বরণ রেখার ট্যাঙ্গেন্টের ঢাল।
চিত্র ২.২: অবস্থান-সময় গ্রাফ বিভিন্ন গতির জন্য
(ক) ধনাত্মক ত্বরণ;
(খ) ঋণাত্মক ত্বরণ; এবং
(গ) শূন্য ত্বরণ।
এখন আমরা কিছু সাধারণ ক্ষেত্রে বেগ-সময় গ্রাফ কেমন দেখায় তা দেখব।
চিত্র ২.৩ ত্বরণ ধ্রুবক থাকার সময় বেগ-সময় গ্রাফকে নিম্নলিখিত ক্ষেত্রে দেখায়:
(ক) একটি বস্তু ধনাত্মক দিক দিয়ে চলেছে এবং ত্বরণও ধনাত্মক।
(খ) একটি বস্তু ধনাত্মক দিক দিয়ে চলেছে কিন্তু ত্বরণ ঋণাত্মক।
(গ) একটি বস্তু ঋণাত্মক দিক দিয়ে চলেছে এবং ত্বরণও ঋণাত্মক।
(ঘ) একটি বস্তু সময় পর্যন্ত ধনাত্মক দিক দিয়ে চলেছে, তারপর একই ঋণাত্মক ত্বরণ নিয়ে বিপরীত দিকে ফিরে গেছে।
যেকোনো গতিশীল বস্তুর জন্য বেগ-সময় গ্রাফের একটি মজার বৈশিষ্ট্য হলো:
গ্রাফের নিচের ক্ষেত্রফল নির্দিষ্ট সময় অন্তরালে সরণ নির্দেশ করে।
এই বক্তব্যের একটি সাধারণ প্রমাণ ক্যালকুলাসের সাহায্যে প্রয়োজন।
তবে, আমরা এটি ধ্রুবক বেগ থাকার একটি সাধারণ ক্ষেত্রে দেখতে পারি। এর বেগ-সময় গ্রাফ চিত্র ২.৪-এ দেখানো হয়েছে।
(ক) ধনাত্মক ত্বরণের সাথে ধনাত্মক দিকে গতি,
(খ) ঋণাত্মক ত্বরণের সাথে ধনাত্মক দিকে গতি,
(গ) ঋণাত্মক দিকে গতি এবং ঋণাত্মক ত্বরণ,
(ঘ) একটি বস্তু যার ঋণাত্মক ত্বরণ আছে এবং যা সময় -এ দিক পরিবর্তন করে। সময় থেকে পর্যন্ত এটি ধনাত্মক -দিকে গতি করে এবং থেকে পর্যন্ত এটি বিপরীত দিকে গতি করে।
চিত্র ২.৪: গ্রাফের নিচের ক্ষেত্রফল নির্দিষ্ট সময় অন্তরালে বস্তুর স্থানান্তরের সমান।
গ্রাফটি সময় অক্ষের সমান্তরাল একটি সরলরেখা এবং থেকে পর্যন্ত এর নিচের ক্ষেত্রফল একটি আয়তক্ষেত্রের ক্ষেত্রফল। আয়তক্ষেত্রটির উচ্চতা এবং ভিত্তি । অতএব, ক্ষেত্রফল = , যা এই সময় অন্তরালে স্থানান্তরের সমান।
এই ক্ষেত্রে কীভাবে একটি ক্ষেত্রফল দূরত্বের সমান হয়? ভাবুন! দুই অক্ষের মানগুলির মাত্রা লক্ষ্য করুন, এবং আপনি উত্তরটি পেয়ে যাবেন।
নোট করুন যে এই অধ্যায়ে বিভিন্ন চিত্রে প্রদর্শিত , , এবং গ্রাফে কিছু স্থানে তীক্ষ্ণ বাঁক দেখা যায়, যা নির্দেশ করে যে ঐ বিন্দুতে ফাংশনগুলো ডিফারেনশিয়েবল নয়। বাস্তব ক্ষেত্রে, ফাংশনগুলো প্রতিটি বিন্দুতে ডিফারেনশিয়েবল হবে এবং গ্রাফগুলো মসৃণ হবে।
এর অর্থ শারীরিকভাবে হলো, ত্বরণ এবং বেগ একটি মুহূর্তে হঠাৎ পরিবর্তন হতে পারে না। পরিবর্তন সর্বদা ক্রমান্বয়ে ঘটে।
২.৪: ধ্রুব ত্বরণের জন্য গতিসূত্র
ধ্রুব ত্বরণের জন্য আমরা কিছু সহজ সমীকরণ বের করতে পারি যা স্থানান্তর (), সময় (), প্রাথমিক বেগ (), চূড়ান্ত বেগ (), এবং ত্বরণ () এর মধ্যে সম্পর্ক স্থাপন করে।
সমীকরণ (২.৪), যা ইতিমধ্যে প্রাপ্ত, একটি বস্তু ধ্রুব ত্বরণ -এর সাথে চলার সময় চূড়ান্ত এবং প্রাথমিক বেগের ( এবং ) মধ্যে সম্পর্ক দেয়:
এই সম্পর্কটি গ্রাফিকভাবে চিত্র ২.৫-এ উপস্থাপিত হয়েছে।
গ্রাফের নিচের ক্ষেত্রফল হলো:
এবং মুহূর্তের মধ্যবর্তী ক্ষেত্রফল = ত্রিভুজ -এর ক্ষেত্রফল + আয়তক্ষেত্র -এর ক্ষেত্রফল।
(ত্রিভুজের ক্ষেত্রফল)+(আয়তক্ষেত্রের ক্ষেত্রফল) =2/1(v−v0)t+v0t
চিত্র ২.৫: ধ্রুব ত্বরণের জন্য একটি বস্তুর গ্রাফের নিচের ক্ষেত্রফল।
পূর্ববর্তী অংশে ব্যাখ্যা করা হয়েছে যে, গ্রাফের নিচের ক্ষেত্রফল বস্তুর স্থানান্তরকে প্রকাশ করে। অতএব, বস্তুর স্থানান্তর হলো:
কিন্তু, , সুতরাং,
অথবা,
সমীকরণ (২.৫) অন্যভাবে লেখা যেতে পারে:
যেখানে,
(শুধুমাত্র ধ্রুব ত্বরণের ক্ষেত্রে)
সমীকরণ (২.৭a) এবং (২.৭b) বোঝায় যে বস্তুটি গড় বেগ, যা প্রাথমিক এবং চূড়ান্ত বেগের গাণিতিক গড়ের সমান, দিয়ে স্থানান্তর সম্পন্ন করেছে।
সমীকরণ (২.৪) থেকে,
এটি সমীকরণ (২.৭a)-তে প্রতিস্থাপন করলে, আমরা পাই:
অথবা,
এবং,
ই সমীকরণটি সমীকরণ (২.৪) থেকে -এর মান সমীকরণ (২.৬)-এ প্রতিস্থাপন করে প্রাপ্ত করা যায়।
এভাবে আমরা তিনটি গুরুত্বপূর্ণ সমীকরণ পাই:
যা পাঁচটি রাশি , , , , এবং -এর মধ্যে সম্পর্ক স্থাপন করে। এগুলো ধ্রুব ত্বরণের জন্য সরলরেখীয় গতির গতিসূত্র।
সমীকরণ (২.৯a) সেটটি ধরে নেওয়া হয়েছে যে, -এ কণাটির অবস্থান । যদি -এ কণাটির অবস্থানের স্থানাঙ্ক শূন্য না হয়, বরং হয়, তবে সমীকরণ (২.৯a) পরিবর্তিত হয় (যেখানে -এর পরিবর্তে প্রতিস্থাপন করা হয়):
উদাহরণ ২.২:
ধ্রুব ত্বরণের জন্য গতিসূত্র ক্যালকুলাস ব্যবহার করে উদ্ভাবন করুন।
উত্তর:
পূর্বนิধারণ অনুযায়ী,
অথবা,
উভয় পাশে ইন্টিগ্রেশন করলে,
(এখানে ধ্রুবক),
অথবা,
আবার,
অথবা,
উভয় পাশে ইন্টিগ্রেশন করলে,
অথবা,
এছাড়া,
অথবা,
উভয় পাশে ইন্টিগ্রেশন করলে,
অথবা,
এই পদ্ধতির সুবিধা হলো এটি ধ্রুব নয় এমন ত্বরণের জন্যও ব্যবহার করা যায়।
উদাহরণ ২.৩:
একটি বল একটি বহুতল ভবনের উপর থেকে বেগে উর্ধ্বমুখে নিক্ষেপ করা হয়। বলটি নিক্ষেপের বিন্দু থেকে মাটি পর্যন্ত উচ্চতা । (ক) বলটি কত উচ্চতায় উঠবে? এবং (খ) বলটি মাটিতে আঘাত করতে কত সময় নেবে?
ধরুন ।
উত্তর:
(ক) আমরা -অক্ষটি উর্ধ্বমুখে ধরে নিই এবং শূন্য বিন্দুটি মাটিতে রাখি (চিত্র ২.৬ অনুযায়ী)।
এখন,
বল যদি নিক্ষেপ বিন্দু থেকে উচ্চতায় উঠে, তবে সমীকরণ ব্যবহার করলে,
সমাধান করে পাই,
(খ) এই অংশটি দুইভাবে সমাধান করা যায়। পদ্ধতিগুলো মনোযোগ সহকারে লক্ষ্য করুন।
চিত্র ২.৬
প্রথম পদ্ধতি: প্রথম পদ্ধতিতে, আমরা গতির পথ দুটি অংশে ভাগ করি: উপরের দিকে গতি (A থেকে B) এবং নিচের দিকে গতি (B থেকে C) এবং সংশ্লিষ্ট সময় এবং গণনা করি। যেহেতু B তে গতি শূন্য, আমাদের কাছে:
অথবা,
এটি হল A থেকে B পর্যন্ত যাওয়ার সময়। B থেকে, বা সর্বোচ্চ উচ্চতার বিন্দু থেকে, বলটি মাধ্যাকর্ষণ ত্বরণের অধীনে মুক্তভাবে পড়ে। বলটি ঋণাত্মক -অক্ষের দিকে চলছে। আমরা সমীকরণ ব্যবহার করি:
এখানে,
সমাধান করে,
অতএব, বলটি মাটিতে আঘাত করার আগে মোট সময় হবে
দ্বিতীয় পদ্ধতি: মোট সময়টি দ্বিতীয় পদ্ধতিতেও গণনা করা যেতে পারে, যেখানে বলটির প্রাথমিক এবং চূড়ান্ত অবস্থানের স্থানাঙ্কগুলো শূন্য বিন্দুর সাথে ব্যবহার করা হয় এবং সমীকরণ
ব্যবহার করা হয়।
এখন,
অথবা,
এই কোয়াড্রেটিক সমীকরণটি সমাধান করে,
দ্বিতীয় পদ্ধতিটি আরও ভালো, কারণ এতে আমরা গতির পথ নিয়ে চিন্তা করতে হয় না, কারণ গতিটি ধ্রুব ত্বরণের অধীনে।
উদাহরণ ২.৪: মুক্ত পতন:
মুক্ত পতনের অধীনে একটি বস্তুর গতির আলোচনা করুন। বায়ুর প্রতিরোধ উপেক্ষা করুন।
উত্তর:
পৃথিবীর পৃষ্ঠের কাছাকাছি একটি বস্তুর মুক্তি হলে তা মাধ্যাকর্ষণ শক্তির প্রভাবে নিচের দিকে ত্বরণ পায়। মাধ্যাকর্ষণ ত্বরণের পরিমাণ দ্বারা প্রকাশ করা হয়। যদি বায়ুর প্রতিরোধ উপেক্ষা করা হয়, তবে বস্তুকে মুক্ত পতন বলা হয়। যদি বস্তুর পতনের উচ্চতা পৃথিবীর ব্যাসার্ধের তুলনায় ছোট হয়, তবে কে ধ্রুবক হিসেবে নেওয়া যায়, যার মান ৯.৮ মি/সেকেন্ড²। মুক্ত পতন তাই একটি ধ্রুব ত্বরণের গতির ক্ষেত্রে হয়।
আমরা ধরে নিই যে, গতি -অক্ষ বরাবর হচ্ছে, বা সঠিকভাবে বললে, -অক্ষ বরাবর, কারণ আমরা উপরের দিকে -অক্ষটিকে ধনাত্মক ধরে নিয়েছি। যেহেতু মাধ্যাকর্ষণ ত্বরণ সবসময় নিচের দিকে থাকে, এটি ঋণাত্মক দিকের এবং আমরা পাই
বস্তুটি বিশ্রামে থেকে থেকে মুক্তি পায়। অতএব,
এবং গতির সমীকরণগুলি হল:
এই সমীকরণগুলি সময়ের সাথে সাথে বস্তুর গতি এবং পার হওয়া দূরত্বের সম্পর্ক এবং গতি এবং দূরত্বের মধ্যে সম্পর্ক দেয়। সময়ের সাথে ত্বরণ, গতি এবং দূরত্বের পরিবর্তন চিত্র ২.৭(এ), (বি) এবং (সি)-তে প্রদর্শিত হয়েছে।
চিত্র ২.৭: মুক্তপতনের অধীনে একটি বস্তুর গতি
(ক) ত্বরণ ও সময়ের পরিবর্তন।
(খ) বেগ ও সময়ের পরিবর্তন।
(গ) দূরত্ব ও সময়ের পরিবর্তন।
উদাহরণ ২.৫: গ্যালিলিওর বিজোড় সংখ্যার নিয়ম
“বিশ্রামে থাকা একটি বস্তু যখন পড়ে, সমান সময়ের ব্যবধানে অতিক্রান্ত দূরত্বগুলো বিজোড় সংখ্যার অনুপাত অনুসারে হয় [অর্থাৎ, ১: ৩: ৫: ৭...]।” এটি প্রমাণ করুন।
উত্তর:
ধরি, একটি বস্তু মুক্তপতনে আছে এবং তার গতির সময়কালকে অনেক সমান সময়ের ব্যবধানে () বিভক্ত করা হয়েছে। এই সময়ের মধ্যে বস্তুটি যে দূরত্ব অতিক্রম করে তা বের করতে হবে।
যেহেতু প্রাথমিক বেগ শূন্য, সুতরাং আমাদের কাছে রয়েছে:
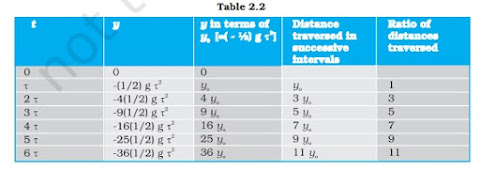
এই সমীকরণ ব্যবহার করে, বিভিন্ন সময় ... এর পরে বস্তুটির অবস্থান নির্ণয় করা যায়। এগুলোকে টেবিল ২.২-এর দ্বিতীয় কলামে দেখানো হয়েছে। যদি আমরা -কে হিসাবে ধরি—যেটি প্রথম সময় -এর পরে অবস্থান নির্দেশ করে, তাহলে তৃতীয় কলামে -এর এককে অবস্থান দেখানো হয়েছে।
চতুর্থ কলামে পরপর সময় -এ অতিক্রান্ত দূরত্ব দেখানো হয়েছে। আমরা দেখতে পাই যে, অতিক্রান্ত দূরত্বগুলো সহজ অনুপাত ১: ৩: ৫: ৭: ৯: ১১... অনুসরণ করে, যা শেষ কলামে দেখানো হয়েছে। এই নিয়মটি গ্যালিলিও গ্যালিলি (১৫৬৪–১৬৪২) প্রতিষ্ঠা করেছিলেন, যিনি মুক্তপতন নিয়ে পরিমাণগত গবেষণা করা প্রথম ব্যক্তি।
উদাহরণ ২.৬: যানবাহনের থামার দূরত্ব
যখন একটি চলন্ত যানবাহনের ব্রেক চাপা হয়, তখন থামার আগে এটি যে দূরত্ব অতিক্রম করে, সেটিকে থামার দূরত্ব বলে। এটি রাস্তার নিরাপত্তার জন্য গুরুত্বপূর্ণ এবং এটি প্রাথমিক বেগ () এবং ব্রেকিং ক্ষমতা বা ব্রেকিং দ্বারা সৃষ্ট ঋণাত্মক ত্বরণ () এর উপর নির্ভর করে।
প্রশ্ন:
এবং -এর উপর ভিত্তি করে থামার দূরত্বের একটি সমীকরণ নির্ণয় করুন।
উত্তর:
ধরি, যানবাহনটি থামার আগে দূরত্ব অতিক্রম করে। তবে, গতি সমীকরণ ব্যবহার করে,
এবং বিবেচনা করে, আমরা পাই:
সুতরাং, থামার দূরত্ব প্রাথমিক বেগের বর্গের সাথে সমানুপাতিক। যদি প্রাথমিক বেগ দ্বিগুণ হয়, তবে থামার দূরত্ব একই ত্বরণের জন্য ৪ গুণ বেড়ে যায়।
একটি নির্দিষ্ট ধরনের গাড়ির ক্ষেত্রে ব্রেকিং দূরত্ব
গাড়িটির থামার দূরত্ব পর্যায়ক্রমে ১০ মিটার, ২০ মিটার, ৩৪ মিটার এবং ৫০ মিটার পাওয়া গেছে, যখন এর গতিগুলো ছিল যথাক্রমে ১১ মিটার/সেকেন্ড, ১৫ মিটার/সেকেন্ড, ২০ মিটার/সেকেন্ড এবং ২৫ মিটার/সেকেন্ড। এই দূরত্বগুলো উপরের সূত্রের সঙ্গে প্রায় সামঞ্জস্যপূর্ণ।
থামার দূরত্ব একটি গুরুত্বপূর্ণ বিষয় যা গতি সীমা নির্ধারণের ক্ষেত্রে বিবেচনা করা হয়, যেমন স্কুল এলাকার ক্ষেত্রে।
উদাহরণ ২.৭: প্রতিক্রিয়া সময়
যখন কোনো পরিস্থিতিতে আমাদের তাৎক্ষণিকভাবে কাজ করা প্রয়োজন হয়, তখন আমরা সাড়া দেওয়ার আগে কিছুটা সময় ব্যয় করি। প্রতিক্রিয়া সময় হলো সেই সময় যা একজন ব্যক্তি পর্যবেক্ষণ, চিন্তা এবং কাজ করতে ব্যয় করেন।
উদাহরণস্বরূপ, যদি একজন ব্যক্তি গাড়ি চালাচ্ছেন এবং হঠাৎ একটি ছেলে রাস্তার মাঝে এসে পড়ে, তাহলে ব্রেক চাপা পর্যন্ত সময়কে প্রতিক্রিয়া সময় বলা হয়।
প্রতিক্রিয়া সময় পরিস্থিতির জটিলতার উপর এবং ব্যক্তির উপর নির্ভর করে।
আপনার প্রতিক্রিয়া সময় পরিমাপ করার একটি সহজ পদ্ধতি
একটি স্কেল নিন এবং আপনার বন্ধুকে এটি আপনার বুড়ো আঙুল ও তর্জনীর ফাঁক দিয়ে লম্বভাবে ফেলার জন্য বলুন (চিত্র ২.৮)। আপনি এটি ধরার পর, স্কেলটি কতটুকু দূরত্ব অতিক্রম করেছে তা মাপুন।
একটি নির্দিষ্ট ক্ষেত্রে, সেন্টিমিটার পাওয়া গেছে। প্রতিক্রিয়া সময় আনুমানিক হিসাব করুন।
সারসংক্ষেপ
- কোনো বস্তু তখনই গতিশীল বলে মনে করা হয়, যখন সময়ের সাথে সাথে তার অবস্থান পরিবর্তিত হয়। বস্তুর অবস্থান একটি সুবিধাজনক উৎস (origin)-এর সঙ্গে তুলনা করে নির্ধারণ করা যায়। সোজা লাইনে গতির ক্ষেত্রে উৎসের ডানদিকে অবস্থান ধনাত্মক এবং বামদিকে অবস্থান ঋণাত্মক ধরা হয়।
কোনো বস্তুর গড় বেগ তার নির্দিষ্ট সময়ে গড় গতির মানের সমান বা বেশি হয়।
তাত্ক্ষণিক গতি বা সাধারণত গতি সংজ্ঞায়িত করা হয় গড় গতির সীমা হিসাবে, যখন সময়ের ব্যবধান () অতি ক্ষুদ্র হয়ে যায়:
কোনো নির্দিষ্ট সময়ে গতি হল অবস্থান-সময় গ্রাফে সেই সময়ে আঁকা স্পর্শকের ঢাল (slope)।গড় ত্বরণ হলো বেগের পরিবর্তনকে সেই সময়ের ব্যবধানে ভাগ করার ফলাফল:
তাত্ক্ষণিক ত্বরণ সংজ্ঞায়িত করা হয় গড় ত্বরণের সীমা হিসাবে, যখন সময়ের ব্যবধান () শূন্যের দিকে যায়:
কোনো নির্দিষ্ট সময়ে ত্বরণ হল বেগ-সময় গ্রাফে সেই সময়ে আঁকা স্পর্শকের ঢাল।
- সামঞ্জস্যপূর্ণ গতির ক্ষেত্রে ত্বরণ শূন্য হয়, এবং অবস্থান-সময় (x-t) গ্রাফ সময় অক্ষের সঙ্গে ঝোঁকা একটি সরলরেখা হয়। বেগ-সময় (v-t) গ্রাফ সময় অক্ষের সমান্তরাল একটি সরলরেখা হয়।
- সামঞ্জস্যপূর্ণ ত্বরণের ক্ষেত্রে অবস্থান-সময় (x-t) গ্রাফ একটি পরাবৃত্ত এবং বেগ-সময় (v-t) গ্রাফ সময় অক্ষের সঙ্গে ঝোঁকা একটি সরলরেখা হয়।
বেগ-সময় গ্রাফের থেকে সময়ের মধ্যে বক্ররেখার নিচের ক্ষেত্রফল বস্তুটির সেই সময়ে স্থানচ্যুতির সমান।
সোজা লাইনে সামঞ্জস্যপূর্ণ ত্বরণের গতির ক্ষেত্রে, পাঁচটি ভৌত রাশি—স্থানচ্যুতি , সময় , প্রাথমিক বেগ , চূড়ান্ত বেগ , এবং ত্বরণ —এর মধ্যে সম্পর্ক নির্ধারণ করা যায় গতিসূত্রের মাধ্যমে:
যদি -এ বস্তুর অবস্থান হয়। যদি কণা -এ শুরু করে, তবে উপরের সমীকরণে -এর স্থানে বসাতে হবে।
মনোযোগ দেওয়ার বিষয়সমূহ
উৎস (origin) এবং অক্ষের ধনাত্মক দিক সম্পূর্ণভাবে আপনার পছন্দের উপর নির্ভর করে। কোনো রাশি, যেমন স্থানচ্যুতি, বেগ এবং ত্বরণের সংকেত নির্ধারণ করার আগে এই পছন্দটি স্পষ্ট করা উচিত।
যদি কোনো কণার গতি বাড়ে, তাহলে ত্বরণ বেগের দিকেই থাকে; আর যদি তার গতি কমে, তবে ত্বরণ বেগের বিপরীত দিকে থাকে। এই বিবৃতি উৎস এবং অক্ষের দিক নির্বাচন থেকে স্বাধীন।
ত্বরণের সংকেত থেকে বোঝা যায় না যে কণার গতি বাড়ছে নাকি কমছে। ত্বরণের সংকেত (পয়েন্ট ৩-এ উল্লেখিত) নির্ভর করে অক্ষের ধনাত্মক দিকের পছন্দের উপর।
উদাহরণস্বরূপ, যদি উলম্বভাবে উপরের দিককে অক্ষের ধনাত্মক দিক হিসেবে ধরা হয়, তাহলে মাধ্যাকর্ষণজনিত ত্বরণ ঋণাত্মক হবে।
- যদি কোনো কণা মাধ্যাকর্ষণে নিচে পড়ে, তবে এই ঋণাত্মক ত্বরণ সত্ত্বেও তার গতি বাড়বে।
- যদি কোনো কণা উপরে নিক্ষেপ করা হয়, তবে একই ঋণাত্মক ত্বরণ তার গতি কমিয়ে দেবে।
কোনো নির্দিষ্ট সময়ে কণার বেগ শূন্য মানে এই নয় যে সেই সময়ে তার ত্বরণও শূন্য। একটি কণা সাময়িকভাবে স্থির থাকতে পারে এবং তবুও তার ত্বরণ শূন্যের চেয়ে বেশি হতে পারে।
উদাহরণস্বরূপ, একটি কণা যখন উপরে নিক্ষিপ্ত হয়, তখন তার সর্বোচ্চ বিন্দুতে তার বেগ শূন্য হয়, কিন্তু সেই সময়েও তার উপর মাধ্যাকর্ষণজনিত ত্বরণ কার্যকর থাকে।গতিসূত্রে (Eq. 2.9) ব্যবহৃত বিভিন্ন রাশি বীজগাণিতিক (algebraic), অর্থাৎ তারা ধনাত্মক বা ঋণাত্মক হতে পারে।
এই সূত্রগুলো সমস্ত পরিস্থিতিতে প্রযোজ্য (যদি গতির মাত্রা একমাত্রিক হয় এবং ত্বরণ ধ্রুবক থাকে), তবে সূত্রে সঠিক সংকেতসহ বিভিন্ন মান প্রতিস্থাপন করা প্রয়োজন।তাত্ক্ষণিক বেগ এবং ত্বরণের সংজ্ঞাগুলো (Eq. 2.1 এবং Eq. 2.3) সুনির্দিষ্ট এবং সর্বদা সঠিক। তবে গতিসূত্রগুলো (Eq. 2.9) কেবল তখনই প্রযোজ্য যখন গতির সময়কালে ত্বরণের মান এবং দিক উভয়ই ধ্রুবক থাকে।














No comments:
Post a Comment